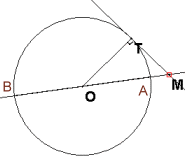
Puissance d'un point par rapport à un cercle
MT² = MA * MB
Si AB est le diamètre de la terre, MT est appelé l'horizon marin du point M, ce qui donne pour l'endroit où j'habite (240 m d'altitude) MT² = 240 * 12713240
MT = 55 237 m
Travail fait à partir d'un courrier de M. Jean-Marie HUGUENIN.
M. Jean-Marie HUGUENIN a pu observer la Corse du centre-helio-marin de Vallauris en février 1948, sa photo prise vers 5h AM a été publiée dans la revue "LA NATURE".
Dans un premier temps il calcule l'horizon marin d'une personne située à une altitude h1, puis il retranche cette valeur à la distance qui la sépare du Monte-Cinto; le reste du calcul se place alors dans un triangle rectangle.
 |
Puissance d'un point par rapport à un cercle MT² = MA * MB Si AB est le diamètre de la terre, MT est appelé l'horizon marin du point M, ce qui donne pour l'endroit où j'habite (240 m d'altitude) MT² = 240 * 12713240 MT = 55 237 m |
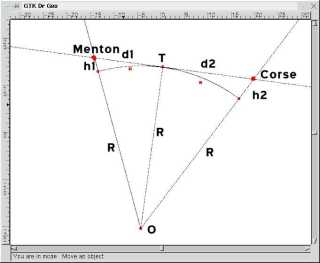 |
Si la distance de Menton au Monte-Cinto MC est de 189 600 m, il reste pour d2 = TC = 189 600 - 55237 = 134 362 m En appliquant le théorème de Pythagore dans le triangle rectangle OTC on trouve 0C = 6 356 500 m. Il suffit alors de retrancher le rayon de la terre pour connaître ce qui est caché de la corse donc ce qui est visible ! |
Ce calcul confirme les autres méthodes, La Corse est bien visible de Menton.
A 250 m d'altitude à Menton on doit donc voir tout ce qui est à une altitude supérieure à 1600 m en Corse. En comparant la photo et le graphique établi par Joel Leroux on se rend compte qu'on en voit plus que prévu. C'est l'objet de l'analyse de Joel Leroux.

 |
|
| Pour m'écrire : delerue@inln.cnrs.fr |