Voit-on la Corse du continent ?
Distance d'un point à une droite

Idée : depuis un point M du continent, on voit un point C situé en Corse à condition que la distance entre la droite (CM) et le centre de la terre O soit supérieure au rayon R de la terre, soit 6 400 km. Proposition de Vincent Dageville Un fichier Word et des fichiers XLS1, XLS2, XLS3, XLS4, XLS sont accessibles.

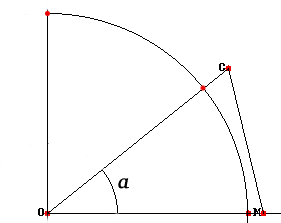
Il suffit donc d'évaluer la différence : D = distance (O, (CM)) - R. Si cette différence est positive, la Corse est visible depuis le point M, si elle est négative, la Corse n'est pas visible depuis M.

En prenant comme distance entre la Corse et le continent 200 km, l'angle a vaut en radians :
(200/2 pi R) x 2 pi = 200/R = 1/32 = 0,03125.

Si (d) est la droite d'équation ux +vy + w = 0, alors la distance entre le point A ( x0 , y0 ) et la droite (d) est égale à :

Comme ici A = O(0 ; 0), la distance vaut : (puisque est un vecteur directeur de (MC))

((R + h) cos a - (R + z) ; (R + h) sin a) = (- b ; a), donc a = (R + h) sin a et b = (R + z)- (R + h) cos a

On en déduit l'équation de la droite (CM) (qui passe par M) :

(R + h) sin a X + [(R + z)- (R + h) cos a] Y = (R + h)(R + z) sin a

On calcule :

MC² = [(R + h) cos a - (R + z)]² + (R + h)² sin²a
= (R + h)² - 2(R + z) (R + h) cos a + (R + z)²

La différence D vaut donc :

D =

C'est cette différence que l'on calculera au tableur en faisant varier l'altitude du point M de 10 m en 10 m et en choisissant pour le point C les altitudes de 1,5 km, 1,8 km, 2 km, 2,2 km, 2,4 km et 2,6 km.

Cette étude montre que les zones de l'île situées au-dessus de 1 800 m sont visibles à partir de l'altitude de 190 m et que celles situées au-dessus de 2 200 m le sont dès l'altitude de 90 m.

Transcription en html d'un texte de Vincent Dageville avec l'éditeur d'équation de StarOffice